| Головна » Статті » Lord Adwond |
Пошук числа Пі інтегруванням: чи можна пришвидшити процес?
| Ми всі зі школи знаємо про таке число Пі, що приблизно дорівнює 3.14. Його можна "прив'язати" до ряду формул: для прикладу, ще із середніх класів мають бути відомі формули знаходження довжини кола та площі круга при відомому радіусі: l=2πr та S=πr2 відповідно. Цими формулами користуватися легко, якщо не брати число Пі наближено, а просто писати його ( тобто його позначення π) як множник. Але інколи, все-таки, доводиться використовувати наближене значення константи. Звідси виникає питання його пошуку. Є різні методи розрахунку наближеного значення числа Пі, але я вирішив дослідити той, що випливає із вище написаної формули, що "прив'язує" дану сталу з площею, яку, в свою чергу, можна "прив'язати" з визначеним інтегралом. Тобто відшукання відомої нам константи можна звести до відшукання визначеного інтеграла. Розглянемо одиничне коло x2+y2=1. Якщо розглянути випадок y>=0, то отримаємо півколо. Якщо розіб'ємо його ще віссю Оу і розглянеми частину, в якій x>=0, то получимо чверть кола. Так як r=1, то площа всього кола рівна π, а отриманої частити π/4. При x є [0; 1] y=sqrt(1-x2), тобто отримуємо, що число π/4 рівне визначеному інтегралу в межах від 0 до 1 з sqrt(1-x2) та π=4*(π/4). Відшукання даного інтеграла неважко запрограмувати за означенням, взявши відрізок xkxk+1 сталим і рівним якомусь сталому числу h, яке назвемо кроком. Я помітив, що при зменшенні кроку значно збільшується кількість обчислень, а разом із ними і час виконання програми. Це викликало питання, що задане у заголовку: чи можна даний алгоритм пришвидшити? Провівши деякі математичні обчислення, моя відповідь - так, і значно. Виявляється, необов'язково інтегрувати на проміжку [0; 1]. Його можна зменшити. Як? За допомогою розбиття кута в 90 градусів на n рівних частин. Нехай α=π/2n. Виконавши таке розбиття розбиття по куту, інтегрування функції sqrt(1-x2) на відрізку [0; 1] можна звести до інтегрування цієї ж функції на проміжку [cos(α); 1]. В чому суть моєї модифікації? Якщо виконати вище згадане розбиття, то даний алгоритм можна звести до відшукання такого S, що π/4=n*S. Позначимо початок координат як точку О і S як суму S1+S2. 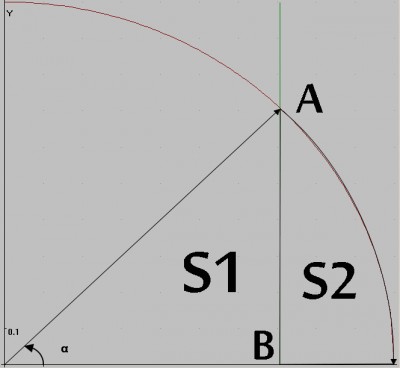 S2 є новим шуканим визначеним інтегралом, а S1=AB*BO/2. AB та BO дорівнюють синусу і косинусу кута α відповідно, тому S1=sin(α)*cos(α)/2. Звідси, підставивши отримані формули у ті, з яких ми починали, получаємо π/4=n*(sin(α)cos(α)/2+S2), де S2 - визначений інтеграл з cos(α) по 1 функції sqrt(1-x2). Запрограмовуємо останню формулу, отримавши її значення, домножуємо його на 4 і все. Як показують мої експерименти, час обчислень дійсно зменшується. Можливо, у когось виникло питання: а наскільки ж цей алгоритм "прискорюється" залежно від n? Теоретично те, в скільки раз можна зменшити час, можна вирахувати за формулою: k=1/(1-cos(α))
Знайдемо, в скільки має скоротитися час розрахунку числа Пі при розбитті чверті кола на n=2, n=3 та n=5 частин. В першому випадку k~10643.9, в другому - k~23948.654, в третьому - k~66523.86.
Надіюсь, даний алгоритм може Вам згодитись. | |
| Переглядів: 278 | | |
| Всього коментарів: 0 | |