| Головна » Статті » Lord Adwond |
Пошук наближених значеннь коренів степеневих рівнянь на ЕОМ
Багато хто, починаючи програмувати, мабуть, задавався питаннями типу "Як наближено знаходити корені степеневого рівняння?". Корені рівняння першого степеня (лінійні) знаходяться простим діленням, другого степеня (квадратні) - через дискримінант. А що робити, коли степінь рівняння вищий від другого? Чи є такі математичні методи наближеного знаходження коренів такого рівняння за умови, що всі вони - дійсні числа?Такі методи є. Я розгляну один з них, який на момент написання цієї статті мені найбільше "по душі".
Виявляється, застосувавши узагальнену теорему Вієта, можна звести пошук наближених значень коренів степеневого рівняння до їх пошуку ітераційними методати розв'язування систем нелінійних рівнянь. А от на вирішення такої задачі є різні методи. Розглянемо такий метод Ньютона, який я час від часу використовую. Він заключається у повторному знаходженні похибок всіх коренів рівняння через розв'язування систем лінійних рівнянь. Спочатку береться вектор Х "початкових" (вхідних) розв'язків. 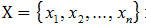 Далі по отриманій за допомогою теореми Вієта системі рівнянь 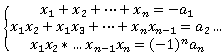 знаходять якобіан і, підставивши замість частинних похідних їх значення та взявши значення з вектора Х, отримують квадратну матрицю. Наступним кроком є розв'язання системи лінійних рівнянь, яка отримується наступним чином (якщо брати матричний запис): в лівій частині отримана квадратна матриця домножується зліва на вектор похибок відповідних коренів, а справа - числовий вектор, утворений зі значень, протилежних до значень функцій-рівнянь при підставлених з вектора Х значень змінних. 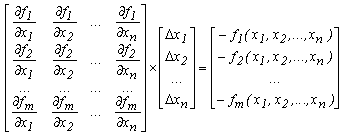 Розв'язавши отриману систему рівнянь, ми получаємо похибки значень коренів. Ми їх додаємо до значень коренів 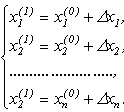 і повторюємо процес доти, доти похибки не задовольнятимуть дану в задачі умову. Чи є інші методи "такого" розв'язання степеневих рівнянь? Звичайно, є. Їх рівно стільки, скільки способів пошуку наближених значень розв'язків систем нелінійних рівнянь. І деякі з них в коді можуть бути менш масивним, ніж розглянутий тут (для прикладу, метод простої ітерації, який за великих степенів може "вимагати" набагато менше коду). І на кінець хочу відмітити ще раз - даний метод (як, в принципі, й інші) працювє за умови, якщо всі корені степеневого рівняння - дійсні числа. Надіюсь, дана інформація Вам згодиться в майбутньому. | |
| Переглядів: 268 | | |
| Всього коментарів: 0 | |